Skip to main content
Published on

OSNR in Next-Gen networks: polarization-resolved optical spectrum analysis allows fast and accurate in-band OSNR measurement

It has become widely accepted that, when applied to next-generation networks, traditional IEC-recommended optical signal-to-noise ratio (OSNR) measurement techniques fail to deliver the required accuracy. As these next-gen networks employ reconfigurable optical add-drop multiplexers (ROADM) and/or multiple-bit/symbol advanced modulation formats (as is the case with most 40 Gbit/s and 100 Gbit/s transmissions), use of traditional OSNR measurements leads to either over- or under-evaluation of the OSNR.

 

When ROADMs were first introduced in the network topology, some commercial optical spectrum analyzers (OSAs) implemented the “polarization-nulling” method to measure OSNR within the filtered dense wavelength-division multiplexing (DWDM) channels. Unfortunately, the complexity of the networks has rendered polarization nulling unsatisfactory in many realistic cases. In this article, we will describe an approach that not only relies on the relative differences in the polarization properties of the data-carrying signal and noise but also leverages their respective spectral properties. What’s more, we will review both methods and discuss their limitations.

Polarization Nulling

The polarization-nulling approach is predicated on the normally realistic assumption that the light signal under test is typically highly polarized and that the superposed noise is not. The measurement setup includes a polarization controller, a polarization splitter and a dual-channel scanning monochromator (i.e. an OSA), as illustrated in Figure 1 (note that detection, signal processing and display electronics have been omitted for the sake of simplicity).

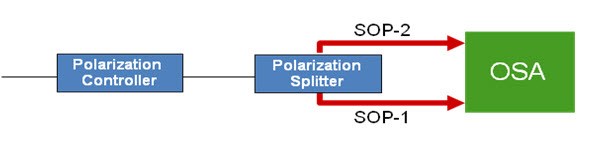
Schematic of an OSA used for the polarization-nulling technique
Figure 1. Schematic of an OSA used for the polarization-nulling technique

The polarization-nulling method involves the adjustment of the (internal) polarization controller in order to extinguish, to the highest degree practicable, the signal in one of the two detection channels of the OSA. Such adjustment corresponds to one of the two outputs of the polarization splitter (acting as a polarizer) to be aligned orthogonally with respect to the (polarized) signal. When this is achieved, the only light reaching the detector of that branch, at that particular wavelength, corresponds to half the noise power (since noise is assumed to be unpolarized, and hence split equally between the two branches).

This provides a measured noise level, and since the OSA also measures the total power (noise + signal), the OSNR for the particular wavelength can be calculated. In order for polarization nulling to provide acceptable measurements, the DWDM channels under test and the OSA itself must meet the following criteria:

  • Polarization-mode dispersion (PMD) on the link should be very modest, preferably near zero. PMD partially depolarizes the signal within the resolution bandwidth (RBW) of the OSA, so complete nulling becomes impossible. In practice, there is some tolerance to PMD, especially if the OSNR that will be measured is not extremely high (e.g., <20 dB) and the RBW of the OSA is very narrow. Nonetheless, it ultimately limits the maximum attainable OSNR values;
  • The polarization optics in the OSA, notably the polarization splitter, must also be able to provide a very high extinction ratio since the maximum measurable OSNR is directly dependent on the extinction ratio;
  • The polarization controller in the OSA must be able to rapidly find, for each of several wavelengths within the DWDM channel, the state of polarization (SOP) condition corresponding to the maximum extinction ratio. However, for OSNR values greater than 20 dB, it can become very time-consuming (i.e., long acquisition times) and in fact, may not even be practical to measure accurately. This is exacerbated when one desires to characterize multiple DWDM channels simultaneously, for instance 16 or more channels extending over much of the C band.

Polarization-Resolved Optical Spectrum OSNR (PROS OSNR)

Like polarization nulling, the polarization-resolved optical spectrum OSNR (PROS OSNR) approach exploits the characteristics of the different degrees of polarization of the signal under test (i.e., the data-carrying signal) and the superposed noise to measure the OSNR within a DWDM channel. Again, as with polarization nulling, a polarization-diverse OSA arrangement (similar to that illustrated in Figure 1) is required to undertake the measurements. However, unlike polarization nulling, which requires (near) complete extinction of the signal in one arm (e.g., 30 dB extinction is required for 20 dB OSNR sensitivity with 0.5 dB uncertainty), a few decibels of difference in the orthogonally-analyzed measured signals of the polarization-diverse OSA suffice to measure an OSNR in excess of 20 dB—and considerably higher OSNR values can be measured with resolved differences greater than 10 dB, which is still far from complete extinction in most cases (e.g., 20 dB OSNR sensitivity with the same 0.5 dB uncertainty can be achieved with less than 5 dB extinction). Hence, nulling of the signal, i.e., essentially complete extinction of the signal in one of the two OSA channels, is not necessary to obtain excellent OSNR sensitivity with the PROS OSNR approach.

As an indication of the degree to which the PROS OSNR method is more efficient, it is frequently asked how the polarization-nulling and the PROS OSNR methods, although both based on a common basic principle (i.e., differential polarization response of the signal versus the noise) and both employing essentially the same measurement hardware, can exhibit such a substantial difference in OSNR measurement performance. To highlight this, an analogy may be useful: a mechanical lever permits a heavy load to be displaced over a short distance by using much lesser force, but this comes at the expense of applying this force over a longer distance. Here, differential polarization response leverages the noise measurement capability at the expense of requiring measurements to be taken over a certain wavelength range. Put another way, provided that the previously mentioned conditions have been satisfied, in principle, polarization nulling can measure the underlying noise level at a single wavelength without the acquisition of an optical spectrum. PROS OSNR, on the other hand, requires measurements to be taken over at least a few wavelengths within the DWDM channel of interest to obtain the noise level. In practice however, the spectrum of the light within the DWDM channel is in any case usually measured with polarization nulling in order to calculate the OSNR from the noise level at the optimal position within the channel and hence, obtaining a spectrally-resolved polarization difference response does not result in any additional practical drawbacks with respect to the polarization-nulling approach.

As mentioned above, instead of requiring one of the two (orthogonally-analyzed) signals detected in the OSA to be completely nulled, polarization-resolved optical spectrum only requires a few decibels of difference, which can be achieved much more rapidly than full nulling. The detected spectra in each OSA channel, comprising of different signal levels but with overall similar noise contribution, are then subtracted from each other. The two noise contributions are equal and hence are cancelled, resulting in a spectrum difference that is proportional to the polarized signal only (i.e., noise-free).

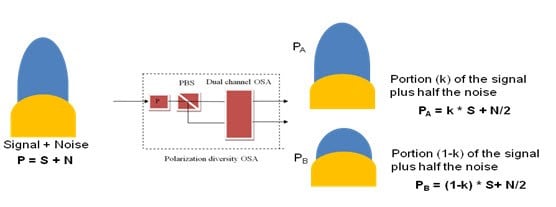
The polarization-diversity approach splits the signal without requiring nulling on either branch
Figure 2. The polarization-diversity approach splits the signal without requiring nulling on either branch

In this way, not only does the OSA acquire the contribution of the signal only (without noise), it also provides the signal shape down to, and even below, the noise level, which contributes to the performance of the polarization-resolved optical spectrum method.

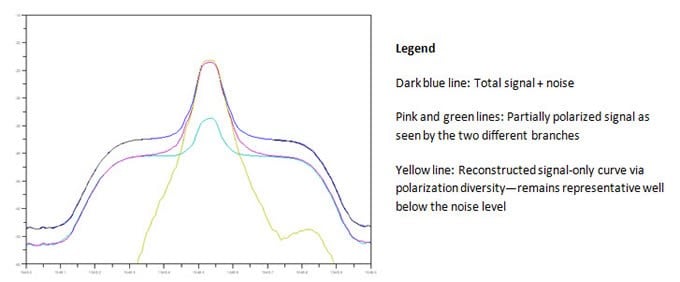
Total signal, cross-polarized signals and reconstructed signal
Figure 3. Total signal, cross-polarized signals and reconstructed signal

Since full polarization extinction is not required, the PROS OSNR approach is much more robust than polarization nulling, since:

  • It is not as susceptible to PMD-induced depolarization (as long as a part of the signal is polarized, sufficient discrimination is achieved) compared to polarization nulling, which assumes a completely polarized signal within the RBW);
  • It is not limited by the polarization-extinction ratio, and hence much larger OSNR can be measured accurately, or equivalently—for a given OSNR sensitivity, the measurement can be performed much more rapidly;
  • It is much faster to achieve a few decibels of diversity than complete nulling of a signal, especially for multiple-wavelength transmission (e.g. DWDM).

In order to fully exploit the PROS OSNR approach, it is important to properly generate the reconstructed signal corresponding to the polarization-resolved difference spectrum, proportional to the (data-carrying) signal but not all the signal. To do so, a proportionality factor must be used to determine the effective contribution of the signal. There are many ways to obtain this proportionality factor: a particularly robust approach, fully exploiting the benefits of PROS OSNR determination, will now be presented in more detail.

With the polarization-resolved optical spectrum approach, the spectrum is acquired at the narrowest OSA resolution bandwidth (RBW), and the subsequent signal processing analysis is carried out with several different numerically-synthesized wider RBWs.

Assuming that the signal spectrum and the noise spectrum have different shapes (ideally, the noise spectrum will not vary in wavelength over most of the data-carrying signal bandwidth), as the RBW increases, the relative contribution of the (data-carrying) signal and noise will vary, and this variation will be more marked on the steep slopes of the (data-carrying) signal spectrum. Analysis of this wavelength-dependent ratio allows the proportionality relation to be determined to complete the signal reconstruction.

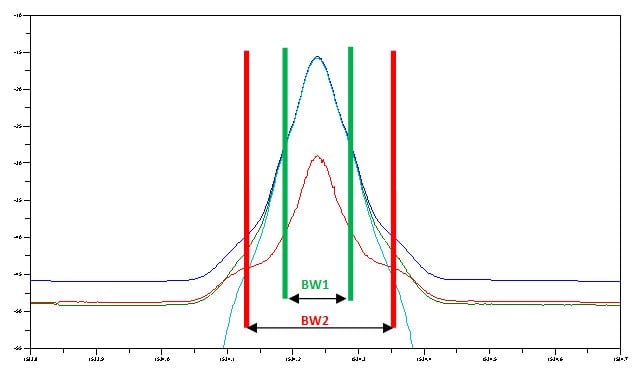
Varying the effective bandwidth by data processing enables more or less power to be included in the analysis
Figure 4. Varying the effective bandwidth by data processing enables more or less power to be included in the analysis

Figure 4 illustrates a signal analyzed using the polarization-resolved optical spectrum OSNR (PROS OSNR) method. First, the channel light is detected using two different effective RBWs (BW1 and BW2). This by itself does not yield relevant signal or noise information, but since the signal shape was reconstructed (light blue curve in Figure 4) using the polarization-resolved optical spectrum method, the signal contribution difference corresponding to the larger bandwidth (BW2) compared to the narrower bandwidth (BW1) is known. Therefore, one can also determine the noise within that bandwidth. Furthermore, since this step is undertaken during post-processing and not during acquisition, several bandwidths may be chosen and analyzed to optimize accuracy and repeatability.

The PROS OSNR analysis helps overcome the practical limitations inherent to the polarization aspects of the technique and allows the determination of the noise profile. Due to its flexibility, notably in finding the proportionality factor for reconstructing the (data-carrying) signal, the PROS OSNR technique yields noise-profile information even when the noise is more narrowly, spectrally carved than the signal spectral extent, as can be the case for example with 40 Gbit/s differential phase-shift keying (DPSK) modulated signals passing through multiple cascaded ROADMs and amplifiers, or when the noise is not split equally between the two branches of the OSA (slightly polarized noise, e.g., from polarization dependent loss (PDL) encountered by the ASE).

Comparing the Approaches

In the cases of either high PMD or high OSNR, PROS OSNR significantly outperforms an approach that is polarization-based only, especially one based solely on polarization nulling. Figure 5 illustrates the performances of three different sets of measurements as a function of OSNR: one based on polarization nulling, the two others use PROS but with different RBWs. The plotted uncertainty comprises both a systematic ‘offset’ from the expected value (based on a carefully pre-calibrated test bed) and a random measurement uncertainty (standard deviation).

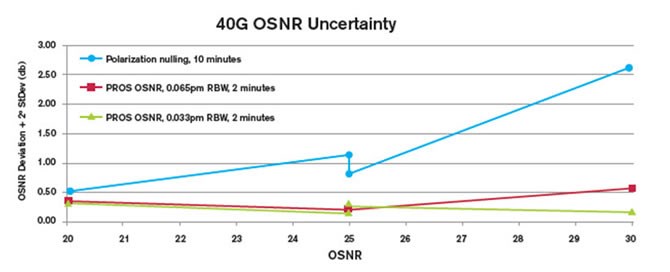
Total OSNR uncertainty vs. OSNR for different OSNR measurement techniques
Figure 5. Total OSNR uncertainty vs. OSNR for different OSNR measurement techniques

As predicted, PROS remains highly accurate for events with high OSNR—with a much faster testing time. As well, for such a measurement approach, a more expensive OSA having very sharp resolution bandwidth does not offer any marked advantages for measuring OSNR.

Figure 6 below shows the same three OSAs at a given OSNR level (25 dB), the presence of PMD induces an additional random measurement uncertainty, which is more significant with the PN method. (To better highlight this additional random PMD-induced uncertainty, the large systematic offset caused by the susceptibility of the polarization nulling method to PMD-induced depolarization is not plotted here.)

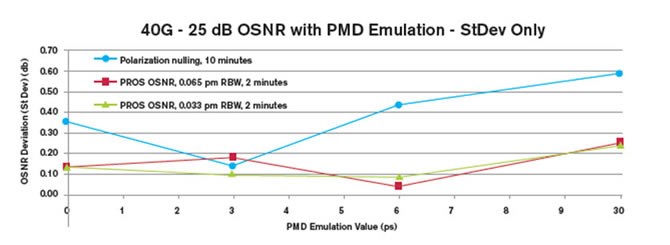
Standard deviations of PMD-induced random uncertainty for different methods (strong-coupled PMD emulator)
Figure 6. Standard deviations of PMD-induced random uncertainty for different methods (strong-coupled PMD emulator)

Hence, in addition to having a limited achievable extinction and thus impaired ability to measure large OSNR, the polarization nulling approach suffers from augmented random uncertainty as the PMD increases. Since most of the advanced modulation formats being employed in next-generation networks tolerate higher link PMD, it will be increasingly important that OSNR measurement on such networks be relatively tolerant to PMD.

Conclusion

Networks are increasing in their complexity, both in terms of cascaded filtering (e.g., via ROADMs in mesh networks) and (OSNR-sensitive) multiple-bit/symbol modulation formats. For instance, intra-channel noise will increasingly be spectrally carved by filters, PMD tolerance of the networks will be increased and the signal bandwidths will frequently be as large as the effective channels widths. But nevertheless, OSNR remains a critical network performance parameter. Purely polarization-based OSNR measurement techniques (e.g., polarization nulling) can perform well when networks and noise sources remain simple, but as demonstrated herein, the robustness and performance of PROS-based OSNR measurement renders it well suited for advanced network architectures and modulation formats.

More insights