下一代网络中的OSNR:偏振解析光谱分析可实现快速精确的带内OSNR测量
在下一代网络中,IEC建议的传统光信噪比(OSNR)测量技术不能实现需要的精度,这一点已经得到了业界的普遍认可。这些下一代网络采用可重构型光分插多路复用器 (ROADM)和/或多位/多符号高级调制模式(大多数40 Gbit/s和100 Gbit/s 传输中的情形),因此使用传统OSNR测量会导致OSNR被高估或低估。
在ROADM最初用于网络拓扑时,一些商用光谱分析仪(OSA)中就引入了“偏振归零”方法来测量经过滤波的密集波分复用(DWDM) 通道中的OSNR。遗憾的是,由于网络比较复杂,使得偏振归零在很多实际情景下都无法满足要求。在本文中,我们将介绍一种新的方法,它不仅依赖于数据承载信号和噪声的偏振属性中所存在的相对差异,而且还会充分利用各自的光谱属性。此外,我们还将比较这两种方法,并且讨论它们各自的不足。
偏振归零
偏振归零方法的基础是一般而言实际存在的这样一个假设:被测光信号通常高度偏振,而叠加噪声却不会。测量装置包括偏振控制器、偏振分光器和双通道扫描单色器(即OSA),如图1所示(请注意,为了简单起见,省略了用于检测、信号处理和显示的电子元器件)。
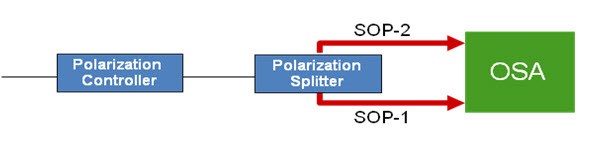
图1. 偏振归零技术所用OSA的示意图
偏振归零方法包括调整(内部)偏振控制器,从而以实际可行的最高程度抑制OSA两个检测通道的其中一个内的信号。这一调整对应于要相对于(偏振)信号正交对准的偏振分光器(用作偏振器)的两个输出中的一个。实现此调整以后,到达该支路的检测器的所有光(特定波长)就对应于一半的噪声功率(由于假设噪声未偏振,因此会在两个支路之间平分)。
这样就能获得实测噪声水平,并且由于OSA还会测量总功率(噪声 + 信号),因此可以计算得出特定波长的OSNR。为了使偏振归零方法提供可接受的测量结果,被测DWDM通道和OSA本身必须满足以下条件:
- 链路上的偏振模色散(PMD)必须非常低,最好接近零。PMD会使OSA分辨率带宽(RBW)中的信号部分消偏振,因此不可能完全归零。实际上,它对PMD有一定的耐受力,尤其是在要测量的OSNR并不是特别高如<20 dB)并且OSA的RBW非常窄的情况下。不过,它最终能测量的最大OSNR也很有限;
- OSA中的偏振光元器件(特别是偏振分光器)也必须具有非常高的消光比,这是因为可以测量的最大OSNR直接取决于消光比;
- 对于DWDM通道内多个波长中的每一个,OSA中的偏振控制器都必须能够快速找到对应于最大消光比的偏振态(SOP)条件。然而,如果OSNR值大于20 dB,此过程将十分耗时(即取样时间会很长),并且实际上可能无法进行准确的测量。如果需要同时鉴定多个DWDM通道,例如,鉴定覆盖C波段大部分的16个或更多个通道,该问题就会更加突出。
偏振解析光谱OSNR(PROS OSNR)
与偏振归零相似,偏振解析光谱OSNR(PROS OSNR)方法也利用被测信号(即数据承载信号)和叠加噪声的不同偏振度这一特征来测量DWDM通道中的OSNR。并且与偏振归零相同的一点是,需要采用偏振分集OSA构造(与图1所示类似)来进行测量。偏振归零要求在偏振分离器一端(接近)完全消除信号(例如,要实现20 dB OSNR敏感度并且不确定度为0.5 dB,需要30 dB的消光比);然而,与偏振归零不同的是,在偏振解析光谱OSNR方法中,只要偏振分集OSA中正交分析的被测信号存在几个分贝的差异,就足以测量超过20 dB的OSNR;另外,如果解析出的差异大于10 dB,就可测量高得多的OSNR值,而10 dB在大多数情况下与完全消除仍然有很大距离(例如,以小于5 dB的消光比即可实现20 dB OSNR敏感度并且不确定度同样为0.5 dB)。因此,利用PROS OSNR方法,并不需要将信号归零(即将两个OSA通道其中之一内的信号基本上完全消除),就能获得优异的OSNR灵敏度。
为了展示PROS OSNR方法的效率要高出多少,人们经常会问,偏振归零和PROS OSNR方法都基于相同的基本原理(即信号与噪声的差分偏振响应),并且采用大体相同的测量硬件,但是为什么它们的OSNR测量性能会存在如此巨大的差异呢?下面的类比或许能够帮助清晰地解答:机械杠杆允许用小得多的力实现较重负载在较短距离上的位移,但代价是施加力的距离更长。在这里,差分偏振响应实现噪声测量功能时,就需要在特定波长范围进行测量。换句话说,假设前面提到的条件得到了满足,那么原则上,偏振归零可以在不对光谱进行取样的情况下测量单个波长的固有噪声水平。另一方面,PROS OSNR要求在所关注DWDM通道内的至少几个波长下进行测量以获得噪声水平。然而在实际中,使用偏振归零的任何情况下通常都会测量DWDM通道中光的光谱,从而根据通道内最优位置的噪声水平计算OSNR;因此,获得光谱解析偏振差异响应这一过程并不会导致任何其他实际缺点(相对于偏振归零方法)。
如上文所述,偏振解析光谱方法不要求将OSA中两个(正交分析的)被检测信号水平中的一个完全归零,而仅仅是要求几个分贝的差异即可,这实现起来要比完全归零快得多。然后分别从两者中减去每个OSA通道中检测到的光谱,这些光谱中包括不同的信号水平,但同时包括大体上相似的噪声成分。两个噪声成分相等,因此会被消除,从而使得到的光谱差异仅与偏振信号成正比(即不含噪声)。
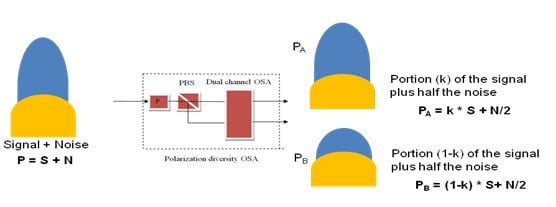
图2. 偏振分集方法在不要求对任何支路归零的情况下分离信号
通过这种方法,OSA不仅会获得仅信号(而不包括噪声)的作用,并且还能提供低至(甚至低于)噪声水平的信号形状,这是偏振解析光谱方法具有很高性能的一个原因。
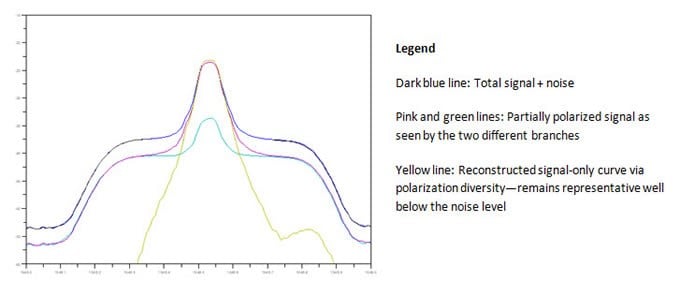
图3. 总信号、正交偏振信号和重建信号
PROS OSNR方法不要求完全消除偏振,因此相对于偏振归零而言稳健得多,具体原因如下:
- 与偏振归零(它假设RBW中的信号完全偏振)相比,不容易受到PMD造成的消偏振效应的影响(只要信号的一部分被偏振,就能足以进行鉴别);
- 不受偏振消光比的限制,因此可以精确测量大得多的OSNR;或者在相同情况下对于给定的OSNR敏感度,能够以快得多的速度执行测量;
- 实现几分贝差异的速度要比将信号完全归零快很多,尤其是在多波长传输(如DWDM)的情况下。
为了充分利用PROS OSNR方法,很重要的一点是正确生成对应于偏振解析差异光谱的重建信号,使其与(数据承载)信号(而不是所有信号)成正比。为此,必须使用某个比例因子来确定信号的有效组成部分。获得这个比例因子有很多方法:现在我们将更加详细地介绍一种尤为稳健的方法,它能充分利用PROS OSNR确定流程所具有的种种优点。
在偏振解析光谱方法中,以最窄的OSA分辨率带宽(RBW)采集光谱,随后使用以数字方式合成起来后更宽的多个不同RBW进行信号处理分析。
假设信号谱和噪声谱具有不同的形状(理想情况下,在大部分数据承载信号带宽内的波长中,噪声谱固定不变),随着RBW增加,(数据承载)信号和噪声的相对成分将发生变化,并且在(数据承载)信号谱很陡峭时,这种变化会更加明显。对依赖于波长的这一比率进行分析,便可确定比例关系,从而完成信号重建。
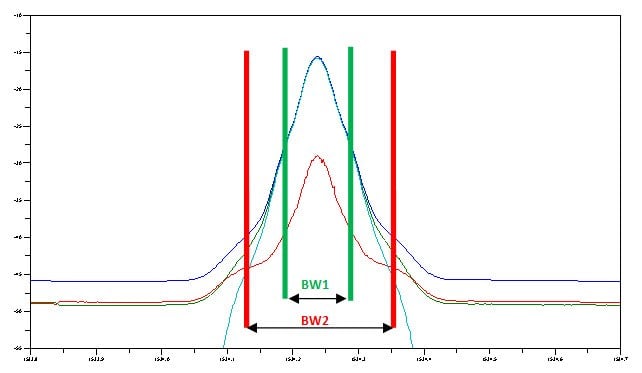
图4. 通过数据处理来改变有效带宽,可以在分析中包含更多或更少功率
图4示出了使用偏振解析光谱OSNR(PROS OSNR)方法分析得出的信号。首先,使用两个不同的有效RBW(BW1和BW2)检测通道中的光。这样做本身并不会得到相应的信号或噪声信息,但由于使用偏振解析光谱方法重建了信号形状(图4中的淡蓝色曲线),因此可以得知对应于较大带宽(BW2)及较窄带宽 (BW1)的信号成分差异。从而也就可以确定该带宽中的噪声。此外,由于该步骤是在后期处理(而不是在取样中)进行,因此可以通过选择和分析多个带宽来优化精度和可重复性。
PROS OSNR分析有助于克服技术层面偏振所固有的实际局限性,并且可以确定噪声特征。PROS OSNR技术极为灵活,尤其是在获取重建(数据承载)信号的比例因子方面,因此,即使是在噪声在光谱上比信号光谱范围窄得多时(如同40Gbit/s 差分相移键控(DPSK)调制信号通过多个级联ROADM和放大器的情形),或者是噪声在OSA两个支路之间未平分(稍微偏振的噪声,例如,ASE产生的偏振相关损耗(PDL)所生成的噪声)的情况下,也能获得噪声特征信息。
几种方法的比较
在PMD较高或OSNR较高的情况下,与仅基于偏振的方法(尤其是仅基于偏振归零的方法)相比,PROS OSNR的效果更为出色。图5显示了三组不同的测量结果(均为OSNR的函数):一组基于偏振归零,另外两组使用PROS,但RBW不相同。所绘制的不确定度包含偏离预期值(基于经过仔细预校准的测试平台)的系统性“偏移”和随机测量不确定度(标准偏差)。
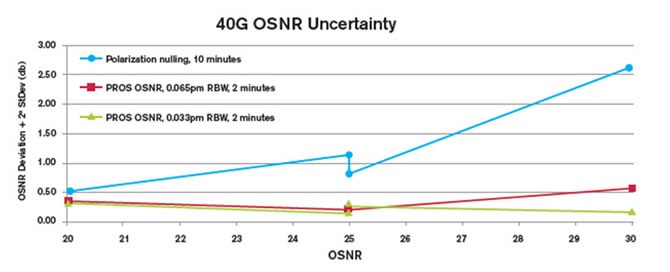
图5. 不同OSNR测量技术的总OSNR不确定度与OSNR对比
正如所预计的一样,对于OSNR较高的事件,PROS仍然有很高的精度,并且测试时间要短得多。此外,对于这类测量方法,分辨率带宽非常灵敏并且价格更为昂贵的OSA并不会在测量OSNR方面带来任何明显的优势。
下面的图6示出了给定OSNR水平(25 dB)下同一OSA的三个结果,由于PMD的存在,造成了与PN方法相比更为显著的额外随机测量不确定度。(为了更好地突出显示PMD造成的这一额外随机不确定度,此处未绘制由于偏振归零方法对于PMD所致消偏振效应敏感而导致的较大系统性偏移。)
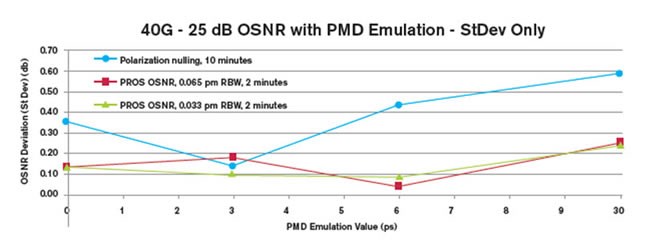
图6. 不同方法下PMD所致随机不确定度的标准偏差(强耦合PMD仿真器)
因此,偏振归零方法不仅在可实现的消光比上有限制(因此测量较大OSNR的能力会受到损害),而且会导致随机不确定度随PMD增加而递增。由于下一代网络中采用的大多数高级调制模式需要容忍更高的链路PMD,因此在这些网络上进行的OSNR测量也相对容忍PMD就变得愈加重要。
结论
不管是在级联滤波(如在网状网络中通过ROADM)还是在(OSNR敏感型)多位/多符号调制模式方面,网络的复杂性都在不断增加。例如,通道内噪声会被滤波器越来越显著地降低,网络的PMD容限会增加,并且信号带宽经常会与有效通道带宽一样大。但无论如何,OSNR仍然是一个关键的网络性能参数。在网络和噪声来源仍然较简单时,完全基于偏振的OSNR测量技术(如偏振归零)有很好的表现,但如本文所讨论,基于PROS的OSNR测量技术稳健可靠,性能强大,特别适合高级网络架构和调制模式。




